Conjunto potencia

El nombre de conjunto potencia proviene del hecho de que si un conjunto A tiene n elementos, la cantidad de subconjuntos que se pueden formar con los elementos de A es 2n. Este conjunto también se conoce como conjunto de partes de un conjunto

Concepto de conjunto potencia

Sean A y X conjuntos cualesquiera; el conjunto formado por todos los subconjuntos de A de denomina conjunto potencia y se denota por P(A). Simbólicamente

Ejemplo: Sean A y B conjuntos definidos como A={2}, B={1,2,3} y C=={ }.

Propiedades del conjunto potencia

Sean A, B, X conjuntos cualesquiera, entonces se tiene:

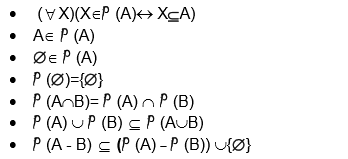
Ejemplo: Demuestre que

Número de elementos de un conjunto

Sea A un conjunto finito; el número de elementos de un conjunto denotado n(A) corresponde a un número natural que indica la cantidad de elementos del conjunto dado.
El cálculo del número de elementos de un conjunto consiste en contar los elementos del conjunto; por lo tanto, se considerarán conjuntos finitos.
Se denominará n(A) al número cardinal de elementos de A o clase de A. Así que los conjuntos que tengan igual número de elementos se podrá llamar conjuntos coordinables o equipotentes, porque se puede establecer una biyección entre sus elementos.
Si se dan conjuntos finitos y se determina el número de elementos de esos conjuntos, también se podrá hallar de otros conjuntos tales como: la unión la intersección, la diferencia y el complemento de dichos conjuntos.

Ejemplo: dados los conjuntos A={b, f, d} y B={2,6,8}, determine la clase a la cuál pertenecen dichos conjuntos.
Los conjunto A y B pertenecen a la clase 3, porque tienen la misma cantidad de elementos: n(A)=3, n(B)=3 y en efecto, son equipotentes o coordinables (forman relación biunívoca).

Número de elementos de la unión de dos conjuntos

Ejemplo: dados los conjuntos A={2,3,5,7} y B={2,4,6,8} y C={1,9}, halle

Número de elementos de la unión de tres conjuntos

Su demostración es bastante extensa sin embargo puede analizarla la igualdad de manera intuitiva con la ayuda de diagramas de Venn. Se podría creer que la igualdad debiese ser

pero esta identidad tiene sus contraejemplos. Presente algunos casos.

Ejemplo 7.28: una encuesta realizada a excursionistas de la ciudad de Medellín entre los últimos 4 años acerca de los que habían visitado a Argentina, Bolivia y Canadá arrojó la siguiente información:

48% había ido a Argentina

46% había ido a Bolivia

30% había ido a Canadá

26% había ido a Argentina y Bolivia

15% había ido a Bolivia y Canadá

13% había ido a Argentina y Canadá

10% había ido a los tres países
Se quiere saber:
a) El porcentaje que no ha ido a ninguno de los tres países

b) El porcentaje que ha ido a los sumo a dos países

c) El porcentaje que ha ido al menos a dos de estos países

d) El porcentaje que ha ido exactamente a un país

e) El porcentaje que ha ido a Argentina y no a Canadá

f) El porcentaje que ha ido a Bolivia o a Canadá, pero no a Argentina

Para hallar solución al problema se toma como recurso el diagrama de Venn para graficar el problema; luego, utilizando las leyes del álgebra proposicional (en algunos casos) y las operaciones de conjuntos lograremos la solución.
En efecto, veamos la gráfica del problema:
Designemos A: Argentina, B: Bolivia y C: Canadá y U: 100% de los encuestados (figura 7.14)
Para graficar tenga en cuenta, que se inicia primeramente con las instrucciones que indican intersección (de pares de conjuntos y de los tres); que se completan los conjuntos dados y que el total, por ningún motivo, debe
ser mayor que 100.
Solución de a: según la gráfica, el porcentaje que no ha ido a ninguno de los tres países es 20%. Observe que está ubicado por fuera de los tres conjuntos.

Solución de b: La palabra “a lo sumo” significa “máximo”; en nuestro problema, donde se pide hallar los que máximo han ido a dos países, es similar a que estén pidiendo los que han ido a 1 ó a 2 países: 3%+15%+5%+16%+19%+12%=70%
Solución de c: La palabra “al menos” significa “mínimo”; en nuestro problema, donde se pide hallar los que mínimo han ido a dos país, es similar a que estén solicitando los que han ido a 2 ó 3 países:
10%+16%+3%+5%=34%
Solución de d: Los que han ido exactamente a uno de estos países son aquellos que viajado únicamente a Argentina o únicamente a Bolivia o únicamente a Canadá. En efecto son: 15%+19%+12%=46%
Solución de e: el porcentaje que ha ido a Argentina y no a Canadá corresponde a la sección que está en A, pero no está en C. Por consiguiente, es:
19%+16%=35%
Solución de f: trascrito el problema al lenguaje simbólico la expresión queda:

Trascribiendo la expresión de este enunciado a la teoría de conjuntos se tiene:

La solución se puede ver en el diagrama de la figura 7.15 se tiene: 15%+5%+12%=32%
Otra forma de resolver este problema es: se utilizan los correspondientes valores de verdad de los conectivos lógicos de la expresión dada en lenguaje simbólico, así: seleccione el conectivo principal de cada paréntesis y el de la expresión escrita y ponga verdadero a esos conectivos. Por lo tanto, para que cada paréntesis sea verdadero, escriba la tabla de valores de verdad de cada proposición según el conectivo lógico; entonces, las proposiciones verdaderas las deja como están y las de valores falso, las niega. En efecto,
(Bx v Cx)^¬Ax V V Como la proposición Bx v Cx es compuesta, determine cuáles son los posibles que toma Bx y Cx para que su disyunción sea verdadera.